高卒程度公務員試験頻出分野【判断推理③】

こんにちは。東京アカデミー静岡校の高卒公務員担当です。
前回は判断推理（課題処理）の頻出分野の一つである対応関係について解説しましたが、今回も引き続き判断推理（課題処理）の頻出分野について解説したいと思います。今回は論理です。

【例題】
次の命題が真であるとき、確実にいえるのはどれか。

ア．理科の好きな人は、数学が好きである。
イ．英語の好きな人は、数学が好きでない。
ウ．社会の好きな人は、理科が好きでない。
エ．国語の好きな人は、数学が好きでない。

1　社会の好きな人は、国語が好きでない。
2　国語の好きな人は、英語が好きでない。
3　数学の好きな人は、社会が好きでない。
4　英語の好きな人は、社会が好きでない。
5　理科の好きな人は、国語が好きでない。

【解説】
前回の例題もそうですが、この問題も頭の中だけで考えていても、なかなか解けないと思います。そこで、命題を矢印を用いて表します。
例えば、アの「理科の好きな人は、数学が好きである。」は、

と表します。
また、イの「英語の好きな人は、数学が好きでない。」は、

と表します。
同様に命題ウ，エも矢印を用いて表すと、
　
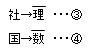
となります。

ここで、論理の問題を解くときに必要な知識として知っておいていただきたいのが対偶です。　
命題「pならばqである。」に対し、「qでないならばpでない。」を対偶といいます。また、元の命題と対偶との真偽は一致します。
例えば、アの「理科の好きな人は、数学が好きである。」の対偶は「数学の好でない人は、理科が好きでない。」となり、真（正しい）であるといえます。

それでは、ア～エの対偶を矢印を用いて表してみます。

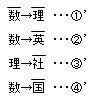
そして、①’～④’はすべて真です。

さらに、論理の問題を解くときに必要な知識として、もう一つ知っておいていただきたいのが、三段論法です。
命題「pならばqである。」，「qならばrである。」が真のとき、「pならばrである。」も真である。これが三段論法です。

この三段論法を用いると、①と④’より、

となります。
これは、「理科の好きな人は、国語が好きでない。」ということですから、正答は5になります。

このように対偶と三段論法を知っていれば、解けそうな気がしませんか。これまで判断推理の頻出分野を紹介してきましたが、いかがでしたか。ただ頭の中で考えているだけでは難しく感じる問題であっても、解法を身に着けておけば解けることが分かっていただけたと思います。さあ、公務員を目指し勉強を始めましょう！

 

公務員になろう！フェア－保護者相談会－　実施中！

只今、東京アカデミーでは「公務員になろう！フェア－保護者相談会－」を実施中です。進路で迷っている方は、是非一度東京アカデミー静岡校にご相談ください。経験豊富なスタッフが、個別で適切なアドバイスをさせていただきます。受付時間は11：00～18：00です。ご希望の方は、お電話または予約フォームからお申込ください。

　フリーコール：0120-220-731　　静岡校直通：054-273-6361

　予約フォームはこちら

オープンキャンパスを開催します！

3月19日(日)の13：00よりオープンキャンパスを実施します。
公務員の仕事についてや試験の勉強法、面接の準備の仕方など公務員試験についてお話していきます。
当日は合格者をお呼びして座談会を実施しますので、これから公務員を目指す方にお勧めのイベントです。

ご希望の方はコチラよりご予約ください。

個別での無料相談も実施しています。個別相談のご予約はこちら